12 Paradox Statements That Will Blow Your Mind

Etymology of paradox statements

It will interest you to know that the word paradox comes from the Greek words “para” – (“against”) and “Doxa” – (“truth” or “opinion”). Paradox statements are an apparently ludicrous or contradictory remark or proposition that, upon closer examination, may turn out to be well-grounded or true.

The word “paradoxon” was employed by Zeno of Elea to describe some of his important intellectual concepts in Plato’s Parmenides, according to the origin of paradox.

We cannot talk about the mathematics of the 20th century, the development of modern logic and set theory without making reference to Russell’s paradox, which states that the set of all those sets that do not contain themselves.

From a mathematical view, to agree that one-half plus one-quarter plus one-eighth plus one-sixteenth and so on… come up to one. It’s the same as stating 0.999 x 1 = 1.

Here are a few more examples of paradox statements:

Paradox statements with numbers

Uninteresting number

An interesting number paradox tells us that the smallest nonzero natural number is 1, the smallest prime number is 2, the first odd prime number is 3, the smallest composite number is 4, and so on. And when you finally arrive at a number that appears to have nothing interesting about it, that number is interesting simply because it is the first number that appears to have nothing intriguing about it. The smallest uninteresting number at the moment is 14,228.

Classroom birthday

There’s a 50-50 chance that at least two people in a classroom of 23 have the same birthday. In a gathering of 75 people, there’s a 99.9% probability that at least two people will match.

Potato weight

A 100-gram potato is 99% water. If it dries to 98% water, it will only weigh 50 grams. The dry components make up 1% of the mass of the potato because it is 99% water. The potato weighs 100 grams, which indicates it has 1 gram of dry matter. When the potato is 98% water, 1 gram of dry matter must now account for 2% of the total weight. Because one gram is 2% of 50 grams, this must be the potato’s new weight.

Infinity Paradox Statements

Tortoise paradox

Maybe the most interesting of Zeno’s paradox statements reads: “In a race, the fastest runner can never overtake the slowest, because the pursuer must first reach the point from where the pursued started, and therefore the slowest always has the advantage.”

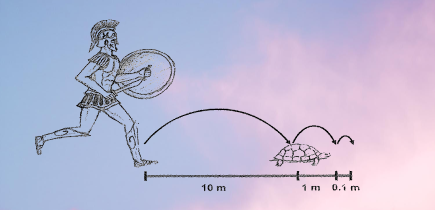
Let’s say that Achilles is 10 times faster and one task will be to reach the point where the tortoise is now. By the time Achilles reaches it, the tortoise will advance. The next task is the reach the tortoise again. The paradox lies in the fact that tasks never end.

Donkey Paradox

Jean Buridan’s famous paradox reads: “If there is a donkey equally distant from the sources of water and food, and the donkey can sense both, but it is equally hungry and thirsty. The donkey will die from both thirst and hunger as it wouldn’t make the decision of where to go first.”

It is like the saying: “It’s all same to me.” Well, it’s hard to imagine a scene where there is no argument about why to choose A over B or vice versa.

Banach-Tarski Paradox

Did you know that you can cut a solid ball into five parts and reassemble them using only stiff motions to create two solid balls that are the same size and shape as the original? Anyone would find this Paradox hard to believe.

Time Travel Paradox

The “traveling twin” of a pair of twins goes to and returns from a very distant place with a speed approaching that of light, while the other (the “Earth-bound twin”) remains at home. Because both twins notice the other twin moving, they both notice that the other is ageing more slowly. As a result, both twins will expect – and discover! – that the other twin is younger when they reunite. An observed moving clock is slow.

Contradiction Paradox Statements

Boat Paradox

Having killed the Minotaur on Crete, Theseus returned to Athens, and they decided to keep his ship as a souvenir. As the time was passing, some parts of the ship had to be replaced. After many years, not a single original part of the ship remains. Is it the same Ship of Theseus?

Court Paradox Statements between Protagoras and his student

Protagoras took on a promising student, Euathlus, with the agreement that the student would pay Protagoras after winning his first case in court. After a while, Euathlus decides that law will not be his profession and begins to study politics. After that decision, Protagoras sued him for unpaid instructions.

Protagoras claimed that if he won the case in court, he would be compensated. Otherwise, if he loses, he will also be paid because this is the first case of Euathlus. On the other hand, Euathlus claims that if he wins the case, he will not have to pay, and if he does not, according to the original agreement, Protagoras should not be paid. Which of the two is right, what would Themis say?

Liar Paradox

The phrase “this statement is a lie” or “this statement is false” is a paradox since, if it were true, it would be saying the opposite. However, if the assertion is true, it would refute the premise that the statement is false. This sentence contradicts itself, indicating that it is true and incorrect at the same time. Isn’t it strange to consider?

Card Paradox Statements

The Card Paradox is a variation of the Liar Paradox, moreover, it illustrates the paradox nicely. There is a card whose front page states:

"The statement on the back side of this card is True."

Looking at the back side of the same card we find the following sentence:

"The statement on the front side of this card is False."

Crocodile Paradox

The Crocodile Paradox has its origins in ancient Greece. In the Middle Ages, the term “crocodilite” was used to describe a similar situation in which your words were used against you, the same as in Contradiction Paradoxes.

Conclusion

To sum up, although paradox statements can be perplexing, accepting opposing viewpoints may be the key to creativity and leadership.