Etimologija paradoksa
Zanimaće vas da riječ paradoks dolazi od grčkih riječi “para” – (“protiv”) i “Doxa” – (“istina” ili “mišljenje”). Paradoksalne izjave su naizgled smiješno ili kontradiktorno zapažanje ili tvrdnja koja se, nakon detaljnijeg razmatranja, može pokazati kao dobro utemeljena ili istinita.
Izstraživajući porijeklo paradoksa nalazimo da je riječ “paradokson” upotrijebio Zenon iz Eleje kako bi opisao neke od svojih važnih intelektualnih koncepata u Platonovom Parmenidu.
Ne možemo govoriti o matematici 20. vijeka, razvoju moderne logike i teorije skupova bez pozivanja na Rusell-ov paradoks, koji kaže da je skup svih onih skupova koji ne sadrže sami sebe.
Sa matematičke tačke gledišta, da se složimo da je polovina plus jedna četvrtina plus jedna osmina plus šesnaesta i tako dalje… dođe do jedan. To je isto kao da navedete 0,999 x 1 = 1.
Evo još nekoliko primjera paradoksalnih izjava:
Paradoksi sa brojevima
Nezanimljiv broj
Zanimljiv paradoks brojeva nam govori da je najmanji prirodni broj različit od nule 1, najmanji prost broj je 2, prvi neparni prost broj je 3, najmanji složeni broj je 4, i tako dalje. A kada konačno dođete do broja za koji se čini da nema ništa zanimljivo, taj broj je zanimljiv jednostavno zato što je to prvi broj za koji se čini da nema ništa intrigantno. Najmanji nezanimljivi broj u ovom trenutku je 14.228.
Rođendan u učionici
Postoji 50-50 šansa da najmanje dvije osobe u učionici od 23 imaju isti rođendan. U skupu od 75 ljudi, postoji 99,9% vjerovatnoća da će se najmanje dvije osobe poklopiti.
Težina krompira
Krompir od 100 grama je 99% vode. Ako se osuši na 98% vode, bit će težak samo 50 grama. Suve komponente čine 1% mase krompira jer je 99% vode. Krompir je težak 100 grama, što znači da ima 1 gram suve materije. Kada je krompir 98% vode, 1 gram suve materije sada mora činiti 2% ukupne težine. Budući da je jedan gram 2% od 50 grama, ovo mora biti nova težina krompira.
Paradoksi Beskonačnosti
Paradoks Kornjače
Možda najzanimljivija Zenonova paradoksalna izjava glasi: „U trci, najbrži trkač nikada ne može prestići najsporijeg, jer progonitelj mora prvo doći do tačke odakle je krenuo, pa stoga najsporiji uvijek ima prednost.
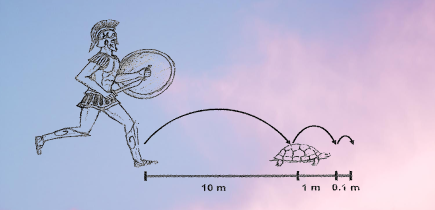
Recimo da je Ahil 10 puta brži i jedan zadatak će biti doći do tačke na kojoj se sada nalazi kornjača. Dok Ahil stigne, kornjača će napredovati. Sljedeći zadatak je ponovno dohvatiti kornjaču. Paradoks leži u činjenici da zadaci nikada ne prestaju.
Magareći Paradoks
Čuveni paradoks Jean Buridan-a glasi: „Ako postoji magarac jednako udaljen od izvora vode i hrane, a magarac može osjetiti i jedno i drugo, ali je jednako gladan i žedan. Magarac će umrijeti i od žeđi i od gladi jer neće donijeti odluku kuda će prije krenuti.”
To je kao izreka: “Meni je to svejedno.” Pa, teško je zamisliti scenu u kojoj nema argumenta zašto odabrati A umjesto B ili obrnuto.
Banach-Tarski Paradoks
Jeste li znali da možete izrezati čvrstu loptu na pet dijelova i ponovo ih sastaviti koristeći samo čvrste pokrete kako biste stvorili dvije čvrste lopte koje su iste veličine i oblika kao original? Bilo kome bi bilo teško povjerovati u ovaj paradoks.
Paradoks blizanaca
„Putujući blizanac” od para blizanaca odlazi i vraća se sa veoma udaljenog mesta brzinom koja se približava brzini svetlosti, dok drugi („blizanac vezan za Zemlju”) ostaje kod kuće. Budući da oba blizanca primjećuju kako se drugi blizanac kreće, oboje primjećuju da drugi sporije stari. Kao rezultat toga, oba blizanca će očekivati – i otkriti! – da je drugi blizanac mlađi kada se ponovo spoje. Uočeni sat koji se kreće je spor.

Kontradiktorni Paradoksi
Paradoks starog broda
Nakon što je ubio Minotaura na Kritu, Tezej se vratio u Atinu, a oni su odlučili da zadrže njegov brod kao suvenir. Kako je vrijeme odmicalo, neki dijelovi broda morali su biti zamijenjeni. Nakon mnogo godina, od broda nije ostao niti jedan originalni dio. Je li to isti Tezejev brod?
Sudski Paradoks Izjava između Protagore i njegovog Učenika
Protagora je preuzeo obećavajućeg studenta, Euathlusa, uz dogovor da će student platiti Protagori nakon što dobije svoj prvi slučaj na sudu. Nakon nekog vremena, Euathlus odlučuje da pravo neće biti njegova profesija i počinje studirati politiku. Nakon te odluke, Protagora ga je tužio zbog neplaćenih instrukcija.
Protagora je tvrdio da će, ako dobije slučaj na sudu, biti obeštećen. U suprotnom, ako izgubi, biće plaćen jer je ovo prvi slučaj Euathlusa. S druge strane, Euathlus tvrdi da, ako dobije spor, neće morati da plati, a ako ne dobije, prema prvobitnom dogovoru, Protagori ne bi trebalo da plati. Ko je od njih dvoje u pravu, šta bi rekla Temida?

“Lažov” Paradoks
Fraza “ova izjava je laž” ili “ova izjava je lažna” je paradoks jer bi, da je istinita, govorila suprotno. Međutim, ako je tvrdnja istinita, to bi opovrglo premisu da je izjava lažna. Ova rečenica je kontradiktorna, ukazujući da je istinita i netačna u isto vrijeme. Nije li čudno?
Paradoks na karti
Paradoks karata je varijacija paradoksa lažova, štaviše, lepo ilustruje paradoks. Postoji kartica na kojoj piše:
"Izjava na poleđini ove karte je tačna."
Gledajući poleđinu iste kartice nalazimo sljedeću rečenicu:
"Izjava na prednjoj strani ove kartice je lažna."
Paradoks krokodila
Paradoks krokodila vuče porijeklo iz antičke Grčke. U srednjem vijeku, termin “krokodilit” se koristio da opiše sličnu situaciju u kojoj su vaše riječi korištene protiv vas, isto kao u paradoksima kontradikcije.
Zaključak
Ukratko, iako paradoksne izjave mogu biti zbunjujuće, prihvatanje suprotnih gledišta može biti ključ kreativnosti i liderstva.9
